↜ Back to index Introduction to Numerical Analysis 1
Part b—Lecture 6
We discuss the other important boundary conditions for the wave equation in one dimension.
Periodic boundary condition
We assume that the solution is 1-periodic function in the x-variable and satisfies the wave equation for all x \in {\mathbb{R}}. In the numerical method, we can express this by treating the values at x_0 and x_M as the same values, and the values at x_{-1} and x_{M-1} as the same values, etc.
Therefore we have only unknowns u_{n,k} for k = 0, \ldots, M-1, n \geq 0. The numerical scheme is \left\{ \begin{aligned} u_{n+1, 0} &= 2u_{n, 0} - u_{n-1,0} + \frac{\tau^2}{h^2} (u_{n, M - 1} - 2 u_{n, 0} + u_{n, 1}),\\ u_{n+1, k} &= 2u_{n, k} - u_{n-1, k} + \frac{\tau^2}{h^2} (u_{n, k - 1} - 2 u_{n, k} + u_{n, k + 1}), && k = 1, \ldots, M-2,\\ u_{n+1, M-1} &= 2u_{n, M-1} - u_{n-1, M-1} + \frac{\tau^2}{h^2} (u_{n, M - 2} - 2 u_{n, M-1} + u_{n, 0}). \end{aligned} \right.
Neumann boundary condition
Now instead of prescribing the value of u at x = 0 and x = 1, we prescribe the value of the derivative u_x = \frac{\partial u}{\partial x}:
\left\{ \begin{aligned} u_{tt}(x, t) &= u_{xx}(x, t), && 0 < x < 1, t > 0,\\ u(x, 0) &= u_0(x), && 0 < x < 1, \\ u_t(x, 0) &= v_0(x), && 0 < x < 1, \\ u_x(0, t) &= a, && 0 < t, \\ u_x(1, t) &= b, && 0 < t. \end{aligned} \right.
This type of boundary condition is called the Neumann boundary condition. We prescribe the value of the derivatives u_x(0, t) = \frac{\partial u}{\partial x}(0, t) and u_x(1, t) = \frac{\partial u}{\partial x}(1, t) on the boundary of the domain, instead of the value of the solution as in the case of the Dirichlet boundary condition.
As in Lecture 3, Neumann boundary condition for the heat equation, we use u_{n, -1} = u_{n, 1} - 2 h a and we use u_{n, M + 1} = u_{n, M-1} + 2 h b. After substituting this into the scheme, we get for k = 0 and k = M the modified scheme
\begin{aligned} u_{n+1, 0} &= 2u_{n, 0} - u_{n-1,0} + \frac{2\tau^2}{h^2} ( u_{n, 1} - u_{n, 0} - h a),\\ u_{n+1, M} &= 2u_{n, M} - u_{n-1,M} + \frac{2\tau^2}{h^2} (u_{n, M-1} - u_{n, M } + h b). \end{aligned}
We also need to modify the initialization for n = 1. For the Dirichlet boundary condition, we used in Lecture 4: u_{1, k} = u_0(x_k) + \tau v_0(x_k) + \frac{\tau^2}{2h^2} \big(u_0(x_{k-1}) - 2 u_0(x_k) + u_0(x_{k+1})\big), \qquad k = 1, \ldots, M - 1. We also need value at k = 0 and k = M. For simplicity, we will assume that u_0 is given on all of {\mathbb{R}} and \frac{\partial {u_0}}{\partial {x}}(0) = a and \frac{\partial {u_0}}{\partial {x}}(1) = b. Therefore we can just take the above scheme for all k = 0, \ldots, M without modification. For example, for k = 0 we just get u_{1, 0} = u_0(x_0) + \tau v_0(x_0) + \frac{\tau^2}{2h^2} \big(u_0(x_{-1}) - 2 u_0(x_0) + u_0(x_1)\big), with u_0(x_{-1}) = u_0(-h).
Stability of the explicit finite difference scheme
As in the Euler method for ordinary differential equations, the time step \tau cannot be taken arbitrarily large in the finite difference scheme for the heat equation.
For the current scheme for the wave equation, \tau and h must satisfy the following stability condition:
Stability condition. \tau \leq h
This is also referred to as the Courant–Friedrichs–Lewy condition.
Note that this is a much weaker restriction than in the case of the heat equation (\tau \leq h^2 /2). However, in practice the wave equation has the form u_{tt} = c^2 u_{xx}, where c is the speed of the waves: the speed of sound or the speed of light, depending on the application. In this case, the stability restriction is \tau \leq \frac h c. Since c is usually very large, the stability restriction is more of an issue.
Exercises
In the following exercises we investigate how the various boundary conditions effect the propagation of waves at the boundary. In all exercises, use the initial data
\begin{aligned} u_0(x) &= f(8 x - 2), &&x \in [0, 1]\\ v_0(x) &= 8f'(8 x - 2), &&x \in [0, 1], \end{aligned} where f(s) := \begin{cases} \exp{\frac 1{s^2 - 1}} & |s| < 1,\\ 0, & \text{otherwise}. \end{cases} and f'(s) is the derivative of f, f'(s) := \begin{cases} -f(s) \frac{2s}{(s^2 - 1)^2} & |s| < 1,\\ 0, & \text{otherwise}. \end{cases} In this case, if there is no boundary, the function u(x,t) = f(8(x+t)-2) is a solution of the wave equation with the above initial data. This is just a traveling wave with a bump shape moving “left” with speed 1.
Exercise 1.
Implement a Fortran program that solves the wave equation with the above initial data and the periodic boundary condition.
Plot the numerical solution with M = 64, h = 1/ M, \tau = h on the time interval t \in [0, 2] using the usual gnuplot’s
splot…with lines.
Submit the plot to LMS with your student ID as the title.
The following exercises will likely appear in Report 2.
Exercise 2.
Implement a Fortran program that solves the wave equation with the above initial data and the Neumann boundary condition u_x(0, t) = u_x(1, t) = 0.
Plot the numerical solution with M = 64, h = 1/ M, \tau = h on the time interval t \in [0, 2] using the usual gnuplot’s
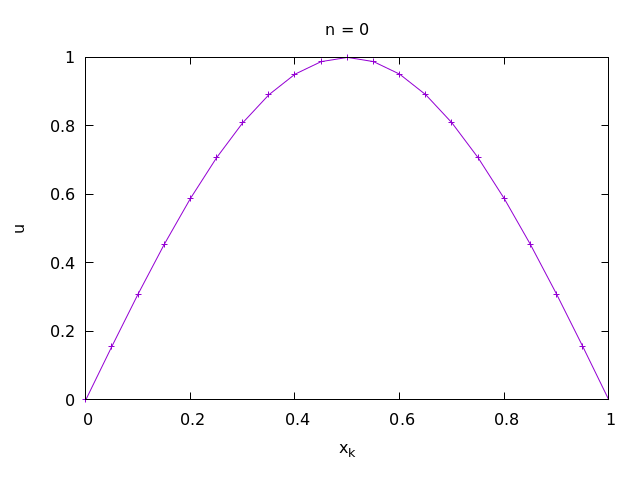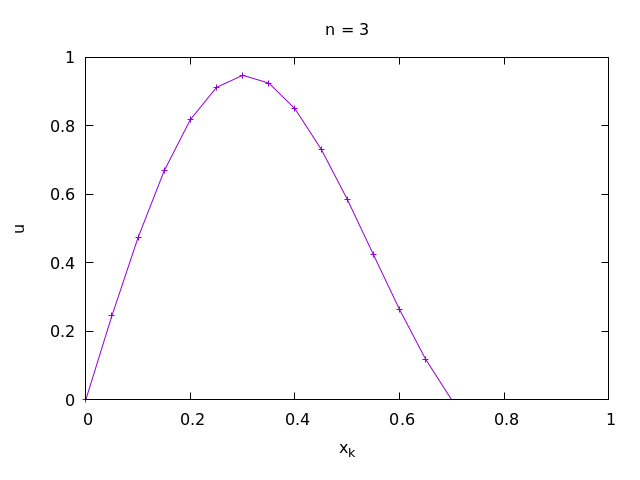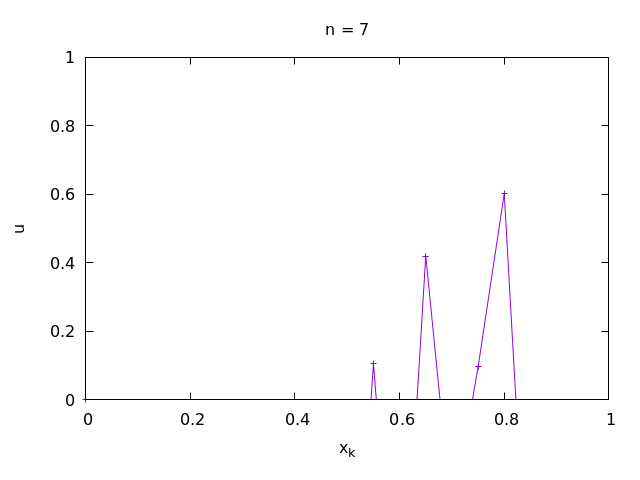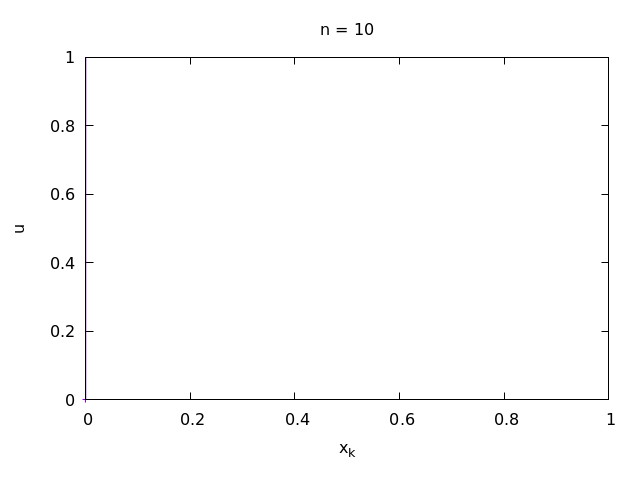
splot…with lines.Plot the numerical solution with the parameters in 2. at time steps n = 9, n =17 and n = 22 in one plot.
Exercise 3.
Implement a Fortran program that solves the wave equation with the above initial data and the Dirichlet boundary condition u(0, t) = 0 at x = 0 and the Neumann boundary condition u_x(1, t) = 0.
Hint. This is a tiny modification of the code of Exercise 2 at k = 0 in the main loop.
Plot the numerical solution with M = 64, h = 1/ M, \tau = h on the time interval t \in [0, 2] using the usual gnuplot’s
splot…with lines.Plot the numerical solution with the parameters in 2. at time steps n = 14, n =16 and n = 25 in one plot.
Example solutions
1-2
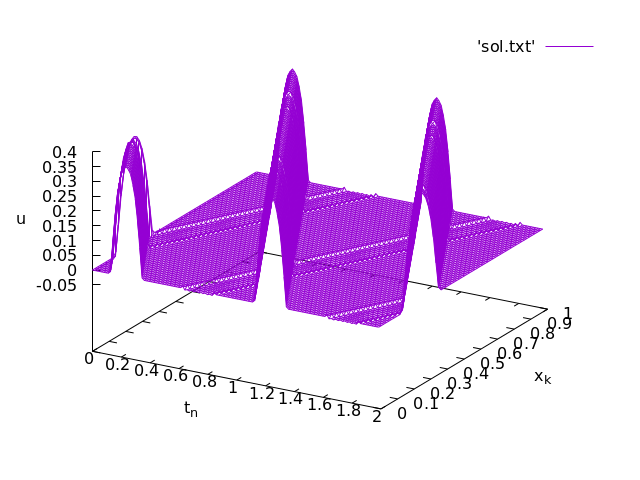
2-2
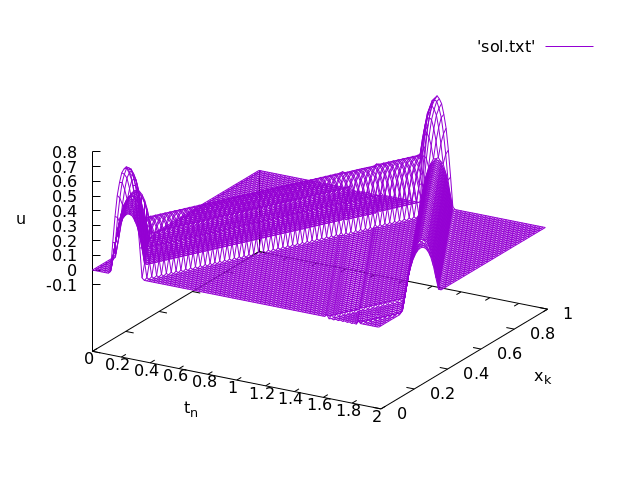
2-3
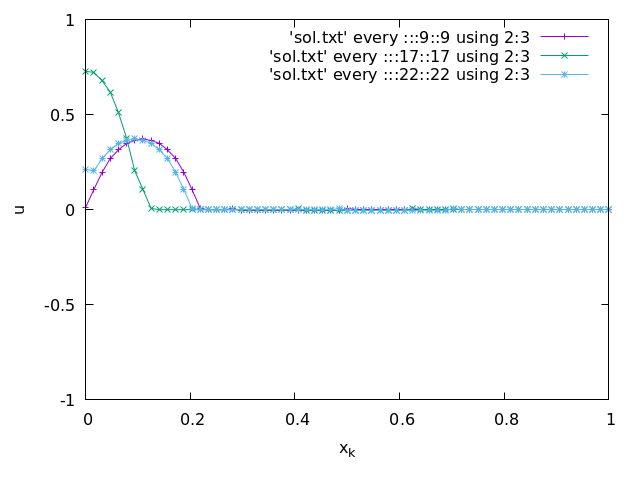
3-2
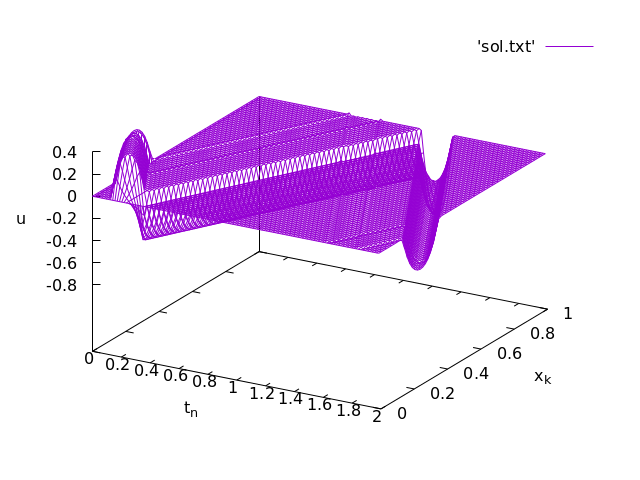
3-3